Integer Number Theory Functions¶

The IntegerNumberTheoryFunctions package contains a variety of operations of interest to number theorists. Many of these operations deal with divisibility properties of integers. (Recall that an integer a divides an integer b if there is an integer c such that b = a * c.)

The operation divisors returns a list of the divisors of an integer.

div144 := divisors(144)
  [1,2,3,4,6,8,9,12,16,18,24,36,48,72,144]
                         Type: List Integer

You can now compute the number of divisors of 144 and the sum of the divisors of 144 by counting and summing the elements of the list we just created.

#(div144)
  15
                         Type: PositiveInteger

reduce(+,div144)
  403
                         Type: PositiveInteger

Of course, you can compute the number of divisors of an integer n, usually denoted d(n), and the sum of the divisors of an integer n, usually denoted sigma(n), without ever listing the divisors of n.

In FriCAS, you can simply call the operations numberOfDivisors and sumOfDivisors.

numberOfDivisors(144)
  15
                         Type: PositiveInteger

sumOfDivisors(144)
  403
                         Type: PositiveInteger

The key is that d(n) and sigma(n) are “multiplicative functions.” This means that when n and m are relatively prime, that is, when n and m have no prime factor in common, then d(nm) = d(n) d(m) and sigma(nm) = sigma(n) sigma(m). Note that these functions are trivial to compute when n is a prime power and are computed for general n from the prime factorization of n. Other examples of multiplicative functions are sigma_k(n), the sum of the k-th powers of the divisors of n and varphi(n), the number of integers between 1 and n which are prime to n. The corresponding FriCAS operations are called sumOfKthPowerDivisors and eulerPhi.

An interesting function is mu(n), the Moebius mu function, defined as follows: mu(1) = 1, mu(n) = 0, when n is divisible by a square, and mu = (-1)^k, when n is the product of k distinct primes. The corresponding FriCAS operation is moebiusMu. This function occurs in the following theorem:

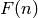Theorem: (Moebius Inversion Formula): Let $f(n)$ be a function on the positive integers and let $F(n)$ be defined by

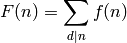
$F(n) = \sum_{d | n} f(n)$

the sum of $f(n)$ over d | n where the sum is taken over the positive divisors of n. Then the values of $f(n)$ can be recovered from the values of $F(n)$

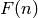
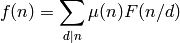
$f(n) = \sum_{d | n} \mu(n) F(n/d)$

where again the sum is taken over the positive divisors of n.

When f(n) = 1, then F(n) = d(n). Thus, if you sum mu(d)..d(n/d) over the positive divisors d of n, you should always get 1.

f1(n)==reduce(+,[moebiusMu(d)*numberOfDivisors(quo(n,d))_
   for d in divisors(n)])
                         Type: Void

f1(200)
  1
                         Type: PositiveInteger

f1(846)
  1
                         Type: PositiveInteger

Similarly, when f(n) = n, then F(n) = sigma(n). Thus, if you sum mu(d)..sigma(n/d) over the positive divisors d of n, you should always get n.

f2(n) == reduce(+,[moebiusMu(d) * sumOfDivisors(quo(n,d))_
   for d in divisors(n)])
                         Type: Void

f2(200)
  200
                         Type: PositiveInteger

f2(846)
  846
                         Type: PositiveInteger

The Fibonacci numbers are defined by ::: F(1) = F(2) = 1 and F(n) = F(n-1) + F(n-2) for n = 3,4,...

The operation fibonacci computes the n-th Fibonacci number.

fibonacci(25)
  75025
                         Type: PositiveInteger

[fibonacci(n) for n in 1..15]
  [1,1,2,3,5,8,13,21,34,55,89,144,233,377,610]
                         Type: List Integer

Fibonacci numbers can also be expressed as sums of binomial coefficients.

fib(n) == reduce(+,[binomial(n-1-k,k) for k in 0..quo(n-1,2)])
                          Type: Void

fib(25)
  75025
                          Type: PositiveInteger

[fib(n) for n in 1..15]
  [1,1,2,3,5,8,13,21,34,55,89,144,233,377,610]
                          Type: List Integer

Quadratic symbols can be computed with the operations legendre and jacobi. The Legendre symbol a/p is defined for integers a and p with p an odd prime number. By definition,

(a/p) = +1, when a is a square (mod p),
(a/p)= -1, when a is not a square (mod p), and
(a/p) = 0, when a is divisible by p.

You compute (a/p) via the command legendre(a,p).

legendre(3,5)
  - 1
                           Type: Integer

legendre(23,691)
  - 1
                           Type: Integer

The Jacobi symbol (a/n) is the usual extension of the Legendre symbol, where n is an arbitrary integer. The most important property of the Jacobi symbol is the following: if K is a quadratic field with discriminant d and quadratic character chi, then chi(n) = (d/n). Thus, you can use the Jacobi symbol to compute, say, the class numbers of imaginary quadratic fields from a standard class number formula.

This function computes the class number of the imaginary quadratic field with discriminant d.

h(d) == quo(reduce(+,[jacobi(d,k) for k in 1..quo(-d, 2)]),2-jacobi(d,2))
                           Type: Void

h(-163)
  1
                           Type: PositiveInteger

h(-499)
  3
                           Type: PositiveInteger

h(-1832)
  26
                           Type: PositiveInteger

Inverse function¶

The inverse function is derived from the Extended Euclidean Algorithm. If we divide one integer by another nonzero integer we get an integer quotient plus a remainder which is, in general, a rational number. For instance,

13/5 = 2 + 3/5

where 2 is the quotient and 3/5 is the remainder.

If we multiply thru by the denominator of the remainder we get an answer in integer terms which no longer involves division:

13 = 2(5) + 3

This gives a method of dividing integers. Specifically, if a and b are positive integers, there exist unique non-negative integers q and r so that

a = qb + r , where 0 <= r < b

q is called the quotient and r the remainder.

The greatest common divisor of integers a and b, denoted by gcd(a,b), is the largest integer that divides (without remainder) both a and b. So, for example:

gcd(15, 5)  = 5,
gcd(7, 9)   = 1,
gcd(12, 9)  = 3,
gcd(81, 57) = 3.

The gcd of two integers can be found by repeated application of the division algorithm, this is known as the Euclidean Algorithm. You repeatedly divide the divisor by the remainder until the remainder is 0. The gcd is the last non-zero remainder in this algorithm. The following example shows the algorithm.

Finding the gcd of 81 and 57 by the Euclidean Algorithm:

= 1(57) + 24
= 2(24) + 9
= 2(9)  + 6
= 1(6)  + 3
= 2(3)  + 0

So the greatest commmon divisor, the GCD(81,51)=3.

If the gcd(a, b) = r then there exist integers s and t so that

s(a) + t(b) = r

By back substitution in the steps in the Euclidean Algorithm, it is possible to find these integers s and t. We shall do this with the above example:

Starting with the next to last line, we have:

3 = 9 -1(6)

From the line before that, we see that 6 = 24 - 2(9), so:

3 = 9 - 1(24 - 2(9)) = 3(9) - 1(24)

From the line before that, we have 9 = 57 - 2(24), so:

3 = 3( 57 - 2(24)) - 1(24) = 3(57) - 7(24)

And, from the line before that 24 = 81 - 1(57), giving us:

3 = 3(57) - 7( 81 - 1(57)) = 10(57) -7(81)

So we have found s = -7 and t = 10.

The Extended Euclidean Algorithm computes the GCD(a,b) and the values for s and t.

Suppose we were doing arithmetics modulo 26 and we needed to find the inverse of a number mod 26. This turned out to be a difficult task (and not always possible). We observed that a number x had an inverse mod 26 (i.e., a number y so that xy = 1 mod 26) if and only if gcd(x,26) = 1. In the general case the inverse of x exists if and only if gcd(x, n) = 1 and if it exists then there exist integers s and t so that

sx + tn = 1

But this says that sx = 1 + (-t)n, or in other words,

sx == 1 mod n

So, s (reduced mod n if need be) is the inverse of x mod n. The extended Euclidean algorithm calculates s efficiently.

Finding the inverse mod n¶

We will number the steps of the Euclidean algorithm starting with step 0. The quotient obtained at step i will be denoted by qi and an auxillary number, si. For the first two steps, the value of this number is given:

s(0) = 0 and
s(1) = 1.

For the remainder of the steps, we recursively calculate

s(i) = s(i-2) - s(i-1) q(i-2) mod n

The algorithm starts by “dividing” n by x. If the last non-zero remainder occurs at step k, then if this remainder is 1, x has an inverse and it is s(k+2). If the remainder is not 1, then x does not have an inverse.

For example, find the inverse of 15 mod 26.

Step 0: 26 = 1(15) + 11 s(0) = 0
Step 1: 15 = 1(11) + 4  s(1) = 1
Step 2: 11 = 2(4) + 3   s(2) = 0  -  1( 1) mod 26 =  25
Step 3: 4  = 1(3) + 1   s(3) = 1  - 25( 1) mod 26 = -24 mod 26 = 2
Step 4: 3  = 3(1) + 0   s(4) = 25 -  2( 2) mod 26 =  21
                       s(5) = 2  - 21( 1) mod 26 = -19 mod 26 = 7

Notice that 15(7) = 105 = 1 + 4(26) == 1 (mod 26).

Using the half extended Euclidean algorithm we compute 1/a mod b.

inverse:(INT,INT)->INT
                            Type: Void

inverse(a,b) ==
  borg:INT:=b
  c1:INT := 1
  d1:INT := 0
  while b ~= 0 repeat
    q := a quo b
    r := a-q*b
    print [a, "=", q, "*(", b, ")+", r]
    (a,b):=(b,r)
    (c1,d1):=(d1,c1-q*d1)
  a ~= 1 => error("moduli are not relatively prime")
  positiveRemainder(c1,borg)
                            Type: Void

inverse(15,26)
 [15,"=",0,"*(",26,")+",15]
 [26,"=",1,"*(",15,")+",11]
 [15,"=",1,"*(",11,")+",4]
 [11,"=",2,"*(",4,")+",3]
 [4,"=",1,"*(",3,")+",1]
 [3,"=",3,"*(",1,")+",0]

 7
                            Type: PositiveInteger

Chinese Remainder Algorithm¶

Let m1,m2,...,mr be positive integers that are pairwise relatively prime. Let x1,x2,..,xr be integers with 0 <= xi < mi. Then, there is exactly one x in the interval 0 <= x < m1 ... m2 ... mr that satisfies the remainder equations

irem(x,mi) = xi, i=1,2,...,r

where irem is the positive integer remainder function.

For example, et x1 = 4, m1 = 5, x2 = 2, m2 = 3. We know that
 irem(x,m1) = x1
 irem(x,m2) = x2
where 0 <= x_ < m1 and 0 <= x2 < m2.

By the extended Euclidean Algorithm there are integers c and d such that

c m1 + d m2 = 1

In this case we are looking for an integer such that

irem(x,5) = 4,
irem(x,3) = 2

The algorithm we use is to first compute the positive integer remainder of x1 and m1 to get a new x1:

x1 = positiveRemainder(x1,m1)
 4 = positiveRemainder(4,5)

Next compute the positive integer remainder of x2 and m2 to get a new x2:

x2 = positiveRemainder(x2,m2)
 2 = positiveRemainder(2,3)

Then we compute x1 + m1 ... positiveRemainder(((x2-x1)*inverse(m1,m2)),m2) or

4+5*positiveRemainder(((2-4)*inverse(5,3)),3)

or

4+5*positiveRemainder(-2*2),3)

or

4+5*2

or

This function has a restricted signature which only allows for computing the chinese remainder of two numbers and two moduli.

x1:=4
  4
                        Type: PositiveInteger
m1:=5
  5
                        Type: PositiveInteger
x2:=2
  2
                        Type: PositiveInteger
m2:=3
  3
                        Type: PositiveInteger
result:=chineseRemainder(x1,m1,x2,m2)
  14
                        Type: PositiveInteger

Integer Number Theory Functions¶

Inverse function¶

Finding the inverse mod n¶

Chinese Remainder Algorithm¶

Table Of Contents

This Page

Navigation

Integer Number Theory Functions¶

Inverse function¶

Finding the inverse mod n¶

Chinese Remainder Algorithm¶

Table Of Contents

This Page

Quick search

Navigation