Combinatorial Function

f := operator 'f


 (1)  f
                                                        Type: BasicOperator

D(product(f(i,x),i=1..m),x)


        m           m    f  (i,x)
      ++-++        --+    ,2
 (2)   | |   f(i,x)>     --------
       | |         --+    f(i,x)
      i= 1         i= 1
                                                   Type: Expression Integer

The binomial``(n, r)`` returns the number of subsets of r objects taken among n objects, i.e. n!/(r! * (n-r)!)

The binomial coefficients are the coefficients of the series expansion of a power of a binomial, that is

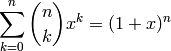
This leads to the famous pascal triangle. First we expose the OutputForm domain, which is normally hidden, so we can use it to format the lines.

)set expose add constructor OutputForm

Next we define a function that will output the list of binomial coefficients right justified with proper spacing:

pascalRow(n) == [right(binomial(n,i),4) for i in 0..n]

and now we format the whole line so that it looks centered:

displayRow(n)==output center blankSeparate pascalRow(n)

and we compute the triangle

for i in 0..7 repeat displayRow i

giving the pretty result:

Compiling function pascalRow with type NonNegativeInteger -> List
   OutputForm
Compiling function displayRow with type NonNegativeInteger -> Void
                                  1
                               1    1
                             1    2    1
                          1    3    3    1
                        1    4    6    4    1
                     1    5   10   10    5    1
                   1    6   15   20   15    6    1
                1    7   21   35   35   21    7    1

See Also:

• )show CombinatorialFunction
• )d op binomial
• )show OutputForm
• )help set